Revisiting Knowledge Distillation via Label Smoothing Regularization 정리

Revisiting Knowledge Distillation via Label Smoothing Regularization

CVPR 2020, 매우 거대한 모델 (cumbersome model) 을 teacher로 활용하여 가벼운 student 모델 (lightweight student model) 을 학습시키는 Knowledge Distillation (KD) 새로운 관점으로 논의 해보는 논문이다. 저자들은 몇가지 observation을 보고하는데:

teacher network 가 student network 를 개선 시킬수 있는 것뿐만아니라, student network 가 teacher network 를 KD 과정을 통해 강화 시킬 수 있다는 실험적인 결과와
student 보다도 좋지 않은 성능을 내도록 poorly-training 된 teacher network 를 사용하더라도 여전히 student network를 향상 시킬 수 있다는 것이다.

이러한 관측 결과를 뒷받침 할 수 있도록 이론적인 부분을 정리하엿는데, KD 와 label smoothing regularization 의 관계 분석을 중심으로:

KD 는 label smoothing regularization 의 한 종류라는것,
label smoothing regularization 이 KD 에서 virtual teacher를 제공한다는 것을 증명한다.

이러한 분석들을 통해, KD 의 성공이 전적으로 teacher 의 category들 간 유사도 정보 때문만이 아니라, soft target 의 regularization 효과도 있으며, 이러한 soft target 의 regularization 효과가 성능 향상에 비슷하거나 더 큰 기여를 한다고 주장한다.

더 나아가 student model 이 teacher 없이 스스로 또는 수동적으로 design 된 regularization distribution 으로 부터 학습할 수 있는 Teacher-free Knowledge Distillation (Tf-KD) framework 를 제안한다.

Introduction

KD 에서 보통 teacher model 은 매우 거대하면서 높은 성능을 가지고, 작은 사이즈의 student model 에게 “soft target” 을 제공하는 방법으로 “teach” 한다.
보통 이러한 “soft target” 을 통해 teacher model 이 축적한 지식 “dark knowledge” 를 student model 에게 전이 할 수 있다고 알려져있다.
이 논문에서는 (1) 반대로 상대적으로 작은 student model 로 부터 나온 “soft target” 을 이용해 teacher model 을 학습 시키도록하고 (2) student model 보다 더 낮은 성능을 내는 poorly-trained teacher model 을 이용해 student model 을 학습 시키도록 한다.
teacher model 의 soft target 을 통해 dark knowledge 를 student model 에게 전이한다는 개념에 기반하자면, 약한 student model 또는 poorly-trained model 의 soft target 을 이용하면 제대로 된 dark knowledge 를 전이 할 수 없을 것이라는 것이 일반적인 생각이다.
하지만, 실험에서는 예상과 달리 이러한 좋지 않은 model 을 통해 KD 를 적용했을 때도 model 이 강화되는 결과를 보여주었고, 이로 인해 KD 의 성공 요인이 knowledge transfer term보다는 regularization term 에 있고 Label Smoothing Regularization (LSR) 과 밀접한 관련이 있다는 것을 시사한다.
결국, 저자들은 실험과 분석을 통해 KD 는 LSR 의 학습된 version 이고 LSR 은 KD 의 ad-hoc 이라는 것을 찾아냈다고 한다. LSR 의 학습된 version 이라는 것은 LSR 은 보통 smoothing parameter 를 manual 하게 주는데 반해, KD 의 teacher 로 부터 나온 smoothed label (soft target) 은 학습이 되어 나왔다는 말이다.

논문은 결론적으로 다음과 같이 정의를 내린다:

“Dark knowledge does not just include the similarity between categories, but also imposes regularization on the student training.”

Exploratory Experiments and Counterintuitive Observations

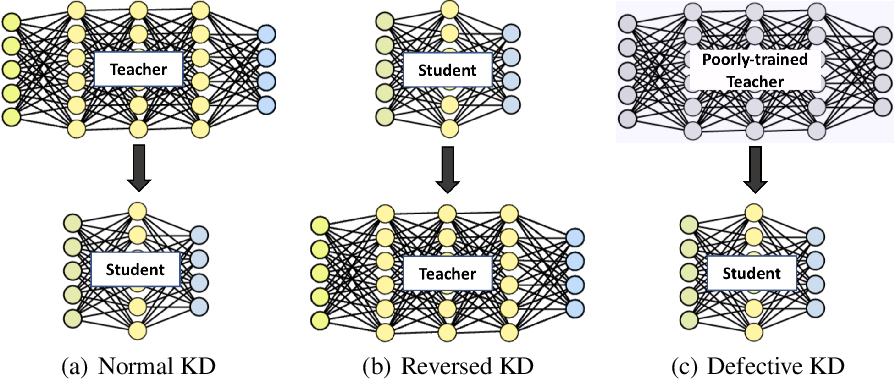
기존과 반대방향, 즉, student –> teacher 방향으로 knowledge 를 전이하는 모델인 Reversed KD, poorly-trained teacher 를 이용한 Defective KD 를 실험한다.

Reversed Knowledge Distillation (Re-KD)

Dataset CIFAR 10, CIFAR 100, Tiny-ImageNet
Student model

5-layer plain CNN, MobilenetV2, ShufflenetV2
Teacher model

ResNet18, ResNet50, DenseNet121, ResNeXt29-8 $\times$ 64d

- CIFAR100 에서의 결과 -

- CIFAR10 에서의 결과 -

- Tiny-ImageNet 에서의 결과 -

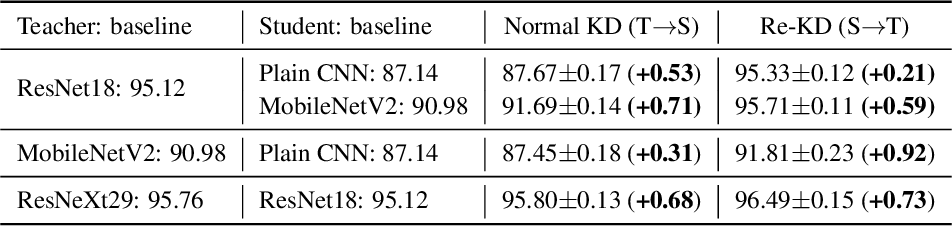
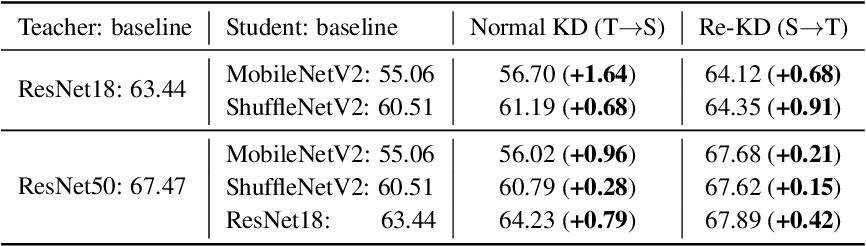
위와 같은 설정으로 진행했을때, 위 결과 표에서 보다시피 student model 이 teacher model의 성능을 향상 시키는 결과를 확인 하였다.

Defective Knowledge Distillation (De-KD)

Dataset CIFAR 100, Tiny-ImageNet
Student model

MobilenetV2, ShufflenetV2
Teacher model

ResNet18, ResNet50, ResNeXt29-8 $\times$ 64d

위 설정에서 teacher model 을 매우 poor 하게 학습시켰다. 논문에서 보고하는 성능은 ResNet18 은 CIFAR100 에서 15.48% 의 정확도, Tiny-ImageNet 에서는 9.41% 의 정확도 밖에 안나오는 정도로 학습을 진행했고, ResNet50 은 각각 45.82% (CIFAR100), 31.01%(Tiny-ImageNet) 의 정확도가 나오는 정도로 학습을 시켰다고 한다.

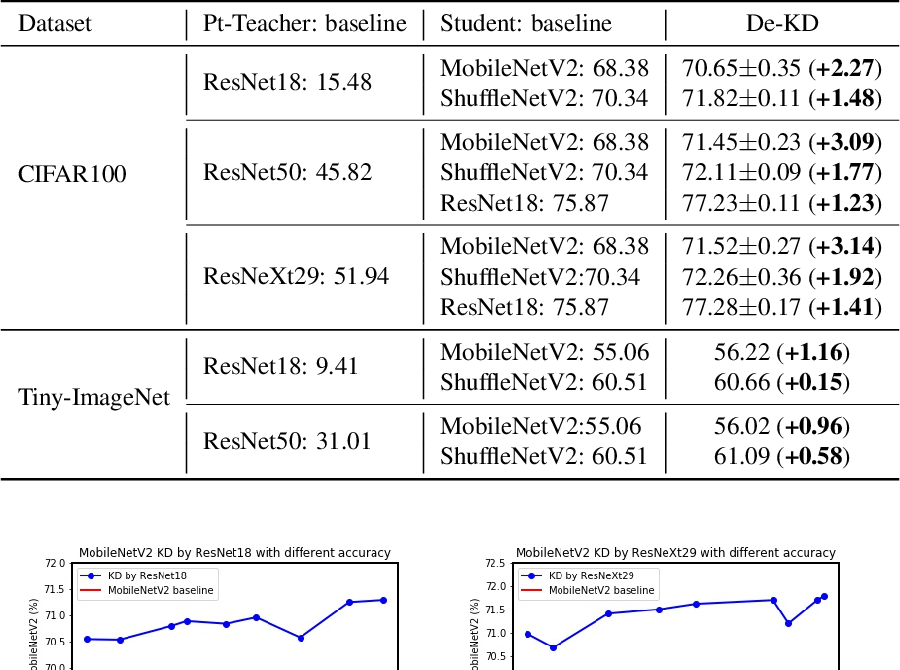
위 결과에서도 보다시피 poorly-trained teacher model 을 이용했음에도 여전히 student model 의 성능향상을 가져온 것을 확인 할 수있다. 결론적으로 teacher 가 noisy 한 logit 을 제공했음에도 student 개선될 수 있다는 것이다.

위 두 실험은 우리가 그 동안 알고있던 직관에 반하는 결과 (counterintuitive result) 라고 볼 수 있다. 이런 결과들로 인해 우리가 그 동안 알고 있던 “dark knowledge” 에 대해 다시 생각하게끔 한다.

흔히 “dark knowledge” 내에 category 정보들이 student model 의 성능 향상을 가져온다고 알고 있었지만, 이러한 category 정보가 부족한 상황에서도 성능 향상을 가져오는 것으로 보아 regularization term 과 연관 지어볼 수 있다. 논문에서는 “dark knowledge” 내 추가적인 정보가 무엇인지 알아보고, KD 와 LSR 사이 관계를 파헤쳐본다.

Knowledge Distillation and Label Smoothing Regularization (KD and LSR)

먼저 KD 와 LSR 사이 관계를 수학적으로 증명하기 위해서 수식적으로 정의를 해보자면,

LSR 은 기존 label distribution $q(k)$ 을 수정한 $q'(k)$ 와 network 의 출력인 $p(k)$ 사이 cross-entropy loss 를 minimize 하는 방식으로 학습을 한다:

$$ q'(k)=(1-\alpha)q(k)+\alpha u(k) $$

이러한 label 을 사용한 cross-entropy loss 인 $H(q',p)$ 는 다음과 같이 정의 된다:

$$ H(q',p)=-\sum^{k}_{k=1}q'(k)log\{p(k)\}=(1-\alpha)H(p,q)+\alpha H(u,p)=(1-\alpha)H(q,p)+\alpha(D_{KL}(u,p)+H(u)) $$

$D_{KL}$ 의 경우 Kullback-Leibler divergence (KL-divergence) 이고 $H(u)$ 는 $u$ 의 entropy 값을 나타내고 고정된 uniform distribution $u(k)$ 이므로 상수 값을 가진다. 결국 Label smoothing을 적용한 loss function 은 상수 term 을 날려버리고 다음과 같이 다시 나타낼 수 있다:

$$ L_{LS}=(1-\alpha)H(q,p)+\alpha D_{KL}(u,p) $$

KD 에서는, teacher network 의 prediction 값 $p(k)$ 를 temperature 파라미터 $\tau$ 로 smooth 하게 조절한 $p^{t}_{\tau}=\frac{exp(z^{t}_{k}/\tau)}{\sum^{K}_{i=1}exp(z^{t}_{i}/\tau)}$ 를 사용하게 된다. 여기서 $z^{t}$ 는 출력으로 나온 logit 값들이다. KD 의 기본 idea 는 student model $S$ 가 다음 수식과 같은 cross-entropy 와 KL divergence 를 minimize 함으로써 teacher model 을 따라하도록 하는 것이다:

$$ L_{KD}=(1-\alpha)H(q,p)+\alpha D_{KL}(p^{t}_{\tau},p_{\tau}) $$

보다시피 LSR 과 KD 의 loss function 을 보면 매우 비슷한 형식을 가지고 있다는 것을 확인 할 수 있다. 단지 차이점은 pre-define 된 $u(k)$ 이냐 teacher 로 학습한 $p^{t}_{\tau}(k)$ 이냐의 차이로 볼 수 있다.

이런 관점에서 KD 는 LSR 의 또 다른 case 라고 볼 수 있으며, LSR 에서 regularization term 인 $D_{KL}(u,p)$ 를 vertual teacher 라고 생각 할 수 있다.

또한 $D_{KL}(p^{t}_{\tau},p_{\tau})=H(p_{\tau}^{t},p_{\tau})-H(p^{t}_{\tau})$ 이기 때문에 고정된 teacher model을 사용했다고 할 때 상수 term 인 $H(p^{t}_{\tau})$ 를 생략하면 다음과 같이 다시 나타낼 수 있다:

$$ L_{KD}=(1-\alpha)H(q,p)+\alpha H(p_{\tau}^{t},p_{\tau}) $$

여기서 우리가 temperature factor $\tau=1$ 로 설정하면, $L_{KD}=H(q^{\sim t},p)$ 이고 $q^{\sim t}$ 는 다음과 같이 나타낼 수 있다:

$$ q^{\sim t}(k)=(1-\alpha)q(k)+\alpha p^{t}(k) $$

이렇게 써놓고 보면, KD 가 LSR 의 한 case 라는 것이 매우 clear 해진다.

결론적으로 정리하자면 다음과 같다:

Knowledge distillation 은 학습된 label smoothing regularization 이다. (A learned label smmothing regularization)
Label smoothing 은 knowledge distillation 의 ad-hoc 이다.
높은 temperature 값에선, teacher의 soft target distribution 은 더 더욱 label smoothing 의 uniform distribution 과 비슷해진다.

이러한 이유들로 인해 앞서 실험한 Re-KD, De-KD 에서도 성능 향상을 이룰 수 있었던 것이다.

Teacher-free Knowledge Distillation (Tf-KD)

“dark knowledge” 가 category 정보를 담고 있다기 보다 label smoothing 의 효과가 크다는 것을 알았다. 그렇다면 teacher model 없이도 이러한 dark knowledge 를 만들 수 있지 않을까라는 생각으로 Tf-KD 를 제안한다.

먼저 self-training knowledge distillation (Tf-KD $_{self}$ ) 을 제안하는데, 이는 Born-again networks 와 매우 유사하다. 차이점으로는 motivation 이 다르고, 이 방법에서는 regularization 으로써 자신으로 부터 나온 soft target 을 이용한다는 것인데… 큰 차이점이라고 말할 순 없을것 같다.
1. 먼저 student model 을 normal 한 방법으로 학습시켜 pre-trained model $S^p$ 을 만든다.
2. $S^{p}$ 의 출력 값을 활용해 동일한 구조의 모델인 $S$ 를 학습시킨다:
  $$ L_{self}=(1-\alpha)H(q,p)+\alpha D_{KL}(p^{t}_{\tau},p_{\tau}) $$
두번째 방법으로는 100% 정확도를 가지는 teacher를 manual 하게 만들어준다. 이게 무슨말이냐면 LSR 같은 경우 기존 ground-truth 를 manual 하게 smoothing 시키면 100% 의 정확도를 가지면서 vertual teacher 가 될 수 있는데 이런 것들을 활용 하겠다는 것이다.
1. 여기서는 KD 와 LSR 을 합친 방법을 사용한다:
  $$ p^{d}(k)=\left\{ \begin{array}{ll} a, & \text{if~}k=c\\ (1-a)/(K-1), & \text{if~}k\not=c. \end{array} \right. $$
  
  여기서 $K$ 는 전체 class의 수이고 $c$ 는 정답 class 이다. $a$ 는 정답 class 일 확률인 것이다. 결국 이전에는 one-hot vector 식으로 무조건 1로 하였는데 여기서는 manual 하게 0.9 이런식으로 soft target을 만들겠다는 것이다. 이게 label 이 smooth 해졌지만 결국 정답에 맞는 확률은 똑같이 가장 높기 때문에 정확도는 100% 가 된다.
이러한 방식을 Teachewr-free KD by manually designed regularization (Tf-KD $_{reg}$ ) 라고 명명하고 다음과 같이 loss 를 정의 하였다:
$$ L_{reg}=(1-\alpha)H(q,p)+\alpha D_{KL}(p^{d}_{\tau},p_{\tau}) $$